本文介绍知识库表示学习中的翻译模型:TransE
预备知识
知识库通常可以看作是三元组的集合,所谓三元组,也就是(头实体,关系,尾实体)的形式,头实体和尾实体统称为实体。下面是几个三元组的例子:
(姚明,出生于,上海)
(姚明,职业,篮球运动员)
(姚明,性别,男)
为了简化起见,我们用(h,r,t)来表示三元组。其中
- h表示头实体
- r表示关系
- t表示尾实体
我们的目标是将知识库中所有的实体、关系表示成一个低维的向量。我们把三元组(h,r,t)对应的向量表示为\((h,r,t)\)。
- \(h\) 表示头实体对应的向量
- \(r\) 表示关系对应的向量
- \(t\) 表示尾实体对应的向量
这样,“姚明”这个实体就不再是一个孤立的符号了,而是一个低维的稠密的向量。它看起来就像下面这样:
[0.01, 0.04, 0.8, 0.32, 0.09, 0.18]
上面这个向量的维度是6维,真实情况下向量的维度会比这个大,但具体取多大并没有一个统一的标准,一般取为50~200左右。
在知识表示中,这种向量有一个专门的名称:embedding。
下面我们就介绍一种将三元组表示成它对应的embedding的方法——TransE。
TransE的基本思想
TransE模型认为一个正确的三元组的embedding\((h,r,t)\)会满足下面的公式:\(h+r=t\)
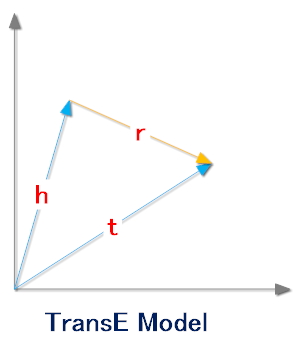
也就是说,头实体embedding加上关系embedding会等于尾实体embedding。同理,如果是一个错误的三元组,那么它们的embedding之间就不满足这种关系。
这就是TransE的基本思想,其实非常的简单。但这却是一种很有效的方法。
TransE的目标函数
上面介绍了transE的基本思想,下面我们介绍如何实现这个想法。 既然我们的目标是学得所有实体和关系的embedding。
上面说了,理想情况下,一个正确的三元组的embedding之间会有\(h+r=t\)的关系,而错误的三元组之间不会有这个关系。因此我们定义如下的势能函数: \(f(h,r,t)=||h+r-t||_2\)
也就是说,我们通过\(h\)和\(t\)之和与\(t\)之差的二范数来表示这个三元组的势能。对于一个正确的三元组,我们希望势能越低越好,而对于一个错误的三元组,我们希望势能越高越好。这样我们就很容易给出目标函数了:
\[min\sum_{(h,r,t)\in\Delta}\sum_{(h',r',t')\in\Delta'}[\gamma+f(h,r,t)-f(h',r',t')]_+\]其中
- \(\Delta\) 表示正确的三元组集合
- \(\Delta'\) 表示错误的三元组集合
- \(\gamma\) 表示正负样本之间的间距,是一个常数
- \([x]_+\) 表示\(max(0,x)\)
为了方便训练,避免过拟合,通常还会在上述目标函数后面增加约束条件 \(||h||\le1,||r||\le1,||t||\le1\)。
负样本(错误三元组)的产生
通常我们得到的知识库是三元组的集合,所有在知识库中出现了的三元组都被看作是正例,那我们如何产生负例呢?我们通常使用替换法来获取负例。
对于三元组\((h,r,t)\),我们随机用知识库中的某个实体\(h'\)来替换\(h\),或者用某个实体\(t'\)来替换\(t\),这样我们就得到了两个负例\((h',r,t)\)和\((h,r,t')\)。
为了避免出现生成的负例其实存在于知识库中的情况,我们可以对生成的负例进行过滤,如果它是知识库中的正例,那我们就不把它作为负例,而是重新生成一个负例。
还有人认为,生成负例的时候不应该在知识库中随机选择一个实体来替换,而是应该选择跟被替换实体类型相似的实体来替换。比如给三元组
(姚明,出生于,上海)
生成负例时,应当在于“上海”类型相似的实体,比如“北京”、“西安”等实体中随机抽取一个来生成负例。因为
(姚明,出生于,上海)
这样的负例比
(姚明,出生于,男)
这样的负例更加合理。
transE的主要内容就是这么多了,后续可能会添加如何编程实现transE的内容。 如何用TensorFlow实现transE可以看这里

This work is licensed under a CC A-S 4.0 International License.